Skip to content
JieWong.com
🌐links

基于重心法的物流中心选址

实验目的及任务

本实验为安徽农业大学信息与计算机学院运筹学实践课大作业，采用重心法和 k-means 聚类算法对安徽省内麦当劳店进行物流中心选址

实验时间为 2023 年 6 月 28 日。

仓库地址：Github

  1. 收集数据
  2. 用重心法计算安徽省内最佳物流中心
  3. 用 K-means 法进行聚类分析

数据收集

收集安徽省内 92 家麦当劳经纬度数据，并把需要配送的需求量化为权重指标。

地址经度纬度权重
麦当劳 (合肥包河万达店)117.31004331.8636348
麦当劳 (合肥之心城店)117.26432431.8598374
麦当劳 (合肥天鹅湖万达店)117.22825531.82704510

用重心法计算安徽省内最佳物流中心

#单重心法.py
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt


# 读取Excel表格数据
data = pd.read_excel('总数据.xlsx')


# 提取经度、纬度和权重列
longitudes = data.iloc[:, 1].values
latitudes = data.iloc[:, 2].values
weights = data.iloc[:, 3].values.astype(float)


# 归一化权重
weights /= np.sum(weights)


# 计算重心
center_longitude = np.dot(longitudes, weights)
center_latitude = np.dot(latitudes, weights)


# 生成可视化图表
plt.scatter(longitudes, latitudes, c='b', label='McDonald\'s')
plt.scatter(center_longitude, center_latitude, c='r', label='Centroid')
plt.xlabel('Longitude')
plt.ylabel('Latitude')
plt.title('Centroid of McDonald\'s Restaurants')
plt.legend()
plt.show()


# 输出重心的经纬度信息
print('Centroid Longitude:', center_longitude)
print('Centroid Latitude:', center_latitude)

程序输出：

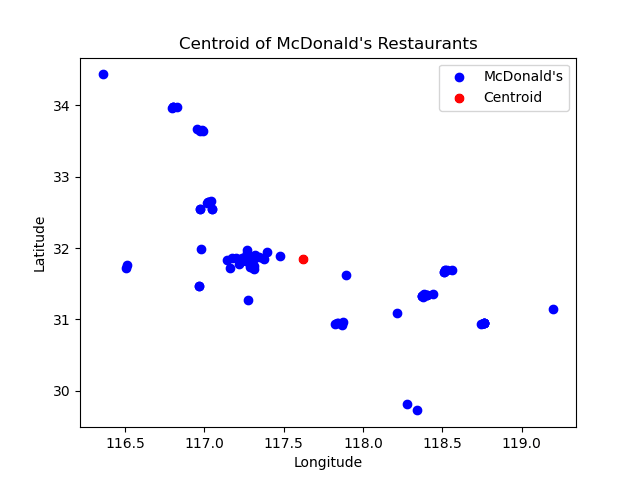
可视化图表 
Centroid Longitude: 117.62247420724346
Centroid Latitude: 31.841021267605637

此处已经获得一个重心坐标 （117.62247420724346,31.841021267605637），即为安徽省内最佳物流中心的坐标。
这个坐标可能是满足全局最优解的一个位置，此地址在地图中为肥东县，如果我们单独划出合肥市区的所有麦当劳，或者仅考虑芜湖市的区域，此坐标不为最优解。
我们进一步所有的局部最优解。

用 K-means 法进行聚类分析

计算 K 值

用轮廓分析法计算 K 值，此处我们只考虑坐标，不考虑权重。

# 轮廓系数zh.py
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
import matplotlib


# 设置中文字体
font_path = 'HarmonyOS_Sans_SC_Black.ttf'  # 替换为你的中文字体文件路径
font = FontProperties(fname=font_path, size=12)
matplotlib.rc('font', family='SimSun')


# 从Excel文件中读取数据
data = pd.read_excel("mdl4.xlsx")


# 提取经度和纬度列数据
coordinates = data.iloc[:, 1:].values


# 设置聚类数目的范围
k_range = range(2, 93)  # 尝试聚类数目从2到93


# 存储每个K值对应的轮廓系数
silhouette_scores = []


# 计算每个K值对应的轮廓系数
for k in k_range:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(coordinates)
    labels = kmeans.labels_
    silhouette_scores.append(silhouette_score(coordinates, labels))


# 设置图形的大小和分辨率
fig, ax = plt.subplots(figsize=(10, 6), dpi=150)


# 绘制K值与轮廓系数的关系图
plt.plot(k_range, silhouette_scores, 'bo-')
plt.xlabel('聚类数目K', fontproperties=font)
plt.ylabel('轮廓系数', fontproperties=font)
plt.title('轮廓系数法确定最佳聚类数目K', fontproperties=font)
plt.show()


# 输出最大的轮廓系数及对应的K值
max_score = max(silhouette_scores)
best_k = k_range[silhouette_scores.index(max_score)]
print("最大的轮廓系数:", max_score)
print("对应的K值:", best_k)

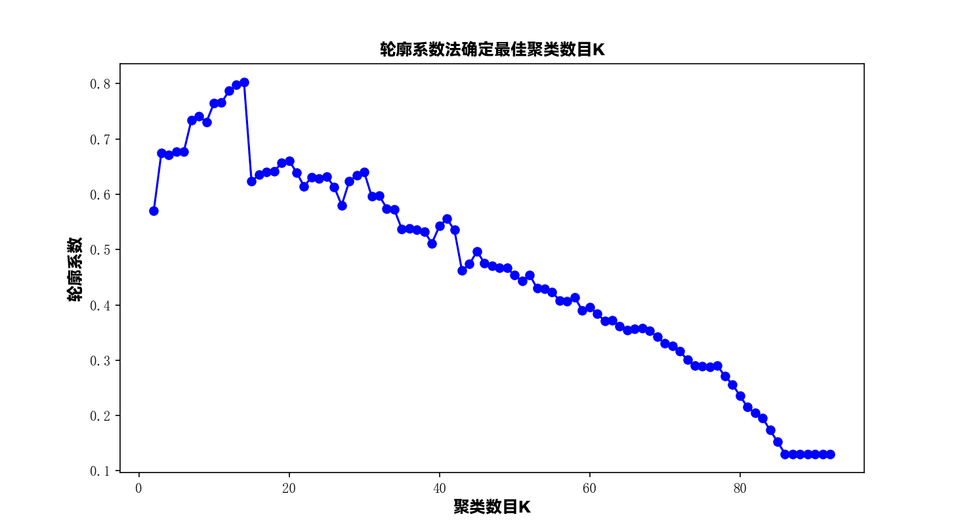
程序输出： 最大的轮廓系数以及 K 值 

最大的轮廓系数: 0.80243070409499
对应的K值: 14

将 K 值带入聚类算法

# 聚类算法.py
import pandas as pd
import numpy as np
import openpyxl
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties, fontManager
from matplotlib.ticker import MultipleLocator


# 查找并选择正确的中文字体
font_path = None
for font in fontManager.ttflist:
    if 'SimSun' in font.name:
        font_path = font.fname
        break


# 设置中文字体
font = FontProperties(fname=font_path, size=12)


# 从Excel文件中读取数据
data = pd.read_excel("mdl4.xlsx")


# 提取经度和纬度列数据
coordinates = data.iloc[:, 1:].values


# 特征缩放
scaler = StandardScaler()
scaled_coordinates = scaler.fit_transform(coordinates)


# 设置聚类数目
k = 14


# 运行K-means算法
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(scaled_coordinates)


# 反向转换聚类中心坐标到原始范围
cluster_centers = scaler.inverse_transform(kmeans.cluster_centers_)


# 输出每个聚类中心坐标
for i, center in enumerate(cluster_centers):
    print("聚类中心", i+1, "经度:", center[0], "纬度:", center[1])


# 创建一个空的字典，用于存储每个聚类中心的点
cluster_points = {i: [] for i in range(k)}


# 将每个数据点分配到相应的聚类中心
labels = kmeans.labels_
for i, label in enumerate(labels):
    cluster_points[label].append(coordinates[i])


# 输出每个聚类中心的所有点到Excel文件
wb = openpyxl.Workbook()
for i in range(k):
    cluster_data = np.array(cluster_points[i])
    sheet = wb.create_sheet(title='Cluster {}'.format(i+1))
    for j, coord in enumerate(cluster_data):
        sheet.cell(row=j+1, column=1).value = coord[0]
        sheet.cell(row=j+1, column=2).value = coord[1]


# 保存Excel文件
wb.save('cluster_points.xlsx')


# 设置图形的大小和分辨率
fig, ax = plt.subplots(figsize=(12, 9), dpi=300)


# 绘制数据点散点图
scatter = ax.scatter(
    coordinates[:, 0],
    coordinates[:, 1],
    c=labels,
    cmap='viridis',
    alpha=0.8,
    s=50,
    linewidths=1
)


# 绘制聚类中心点散点图
ax.scatter(
    cluster_centers[:, 0],
    cluster_centers[:, 1],
    marker='x',
    c='red',
    s=100
)


# 自定义图表
ax.set_xlabel('经度', fontproperties=font)
ax.set_ylabel('纬度', fontproperties=font)
ax.set_title('麦当劳选址聚类结果', fontproperties=font)


# 设置刻度线密度
ax.xaxis.set_major_locator(MultipleLocator(0.2))
ax.yaxis.set_major_locator(MultipleLocator(0.2))


# 添加颜色条图例
cbar = plt.colorbar(scatter)
cbar.set_label('Cluster')


# 调整图表布局并显示图表
plt.tight_layout()
plt.show()

程序输出：
聚类点 

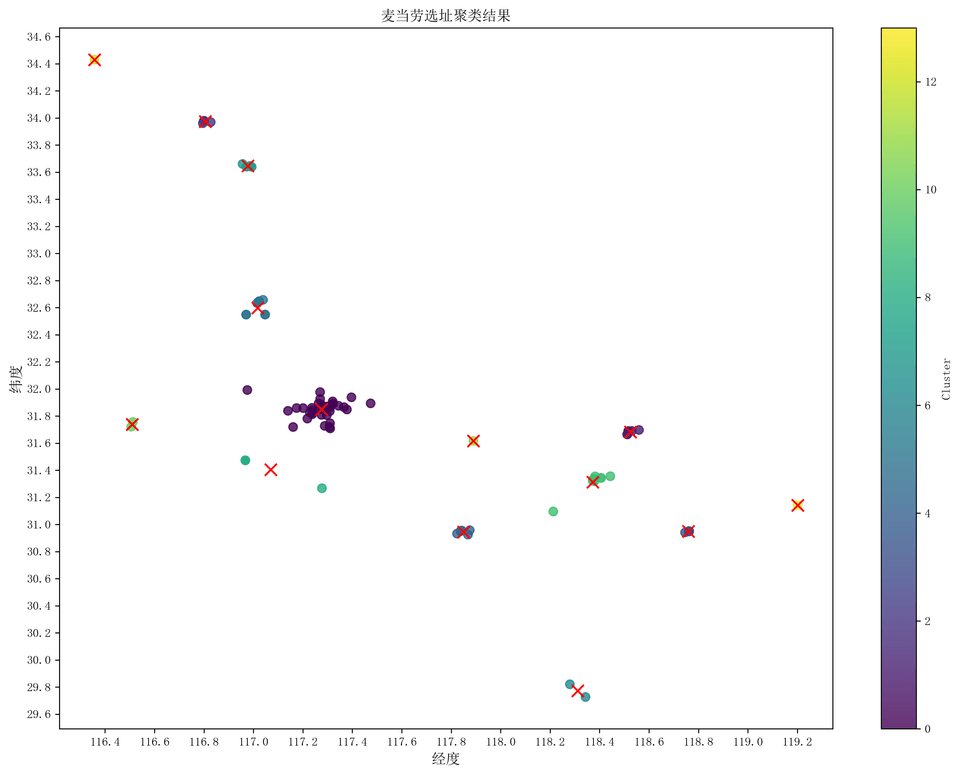
聚类中心 1 经度: 117.27566157894736 纬度: 31.848838526315788
聚类中心 2 经度: 118.5245225 纬度: 31.682757666666667
聚类中心 3 经度: 116.8047722 纬度: 33.973099
聚类中心 4 经度: 118.75912866666667 纬度: 30.948593
聚类中心 5 经度: 117.8492018 纬度: 30.9442564
聚类中心 6 经度: 117.01705925 纬度: 32.597669
聚类中心 7 经度: 118.3117415 纬度: 29.774054
聚类中心 8 经度: 116.976984 纬度: 33.6464185
聚类中心 9 经度: 117.07068766666667 纬度: 31.404715333333332
聚类中心 10 经度: 118.3726679 纬度: 31.3135985
聚类中心 11 经度: 116.50928250000001 纬度: 31.739043000000002
聚类中心 12 经度: 117.890107 纬度: 31.616494
聚类中心 13 经度: 116.357789 纬度: 34.429829
聚类中心 14 经度: 119.20109 纬度: 31.142461

对于生成的 cluster_points.xlsx ，拥有 14 个工作表，每个工作表代表一个聚类中心，包含了该聚类中心的所有点的经纬度信息。

此时可对任一一个聚类中心进行进一步的分析，用单重心法计算最佳物流中心。
如对聚类中心 6 进行分析，可得

Centroid Longitude: 117.27610794021737
Centroid Latitude: 31.850797472826088
© JieWong.com All Rights Reserved.
皖ICP备20013599号-3
皖公网安备34010402704133号