分而治之解决大规模 TSP 问题

本文写于 2024 年，为运筹学高级实践课程大作业。

摘要

摘要

本研究旨在解决大规模旅行商问题（TSP），特别是针对国内众多 5A 级景点的旅游路径规划。由于直接求解大规模 TSP 问题会消耗大量计算资源，因此采用分而治之的策略，首先通过聚类将景点分组，然后分别求解分组顺序和组内最短路径。

1. 引言

在问题规模较大的 TSP 问题中，城市规模较大且节点分布结构复杂，直接通过演化算法求解会造成巨大的资源开销。本文通过将当前巨大的规模 5A 景点聚类成若干个分组，分解 TSP 问题为两个子问题：决定分组之间的顺序和每个已分组内部的最短路径问题。

2. 方法论

2.1 聚类分析

使用 K-means 算法对景点进行聚类。
通过计算轮廓系数确定最佳的聚类数目 K。

2.1.1 K-means 算法

K-means 算法是一种经典的聚类分析方法，用于将数据分为多个类别或 “簇”。其目标是将数据集中的点划分成 K 个簇，使得每个点与其所属簇的中心（即质心）的距离之和最小化。K-means 算法的步骤如下：

初始化：选择 K 个数据点作为初始的簇中心（质心）。
分配：将每个点分配到最近的簇中心，形成 K 个簇。
更新：重新计算每个簇的中心，通常是簇内所有点的均值。
迭代：重复步骤 2 和 3，直到簇中心不再显著变化，或者达到预设的迭代次数。
终止：当簇中心在连续几次迭代中的变化小于某个阈值，或者达到预定的迭代次数时，算法终止。

K-means 算法的关键点包括：

K 的选择：K 是用户根据问题需要预先设定的参数，选择一个合适的 K 值是 K-means 算法中的一个挑战。
初始化方法：簇中心的初始位置对最终的聚类结果有很大影响，常用的初始化方法包括随机选择、K-means++ 等。
收敛性：K-means 算法是迭代的，通常会收敛到局部最优解，但不一定是全局最优。
距离度量：通常使用欧几里得距离来衡量点与簇中心之间的距离，但也可以使用其他距离度量。 K-means 算法简单、快速，适用于大规模数据集，但它也有一些局限性，比如对初始簇中心敏感，且对于噪声和异常值比较敏感。此外，K-means 算法需要事先指定 K 值，但在实际应用中 K 值可能不是显而易见的。在这种情况下，可以使用如轮廓系数等统计度量来帮助确定最佳的 K 值。

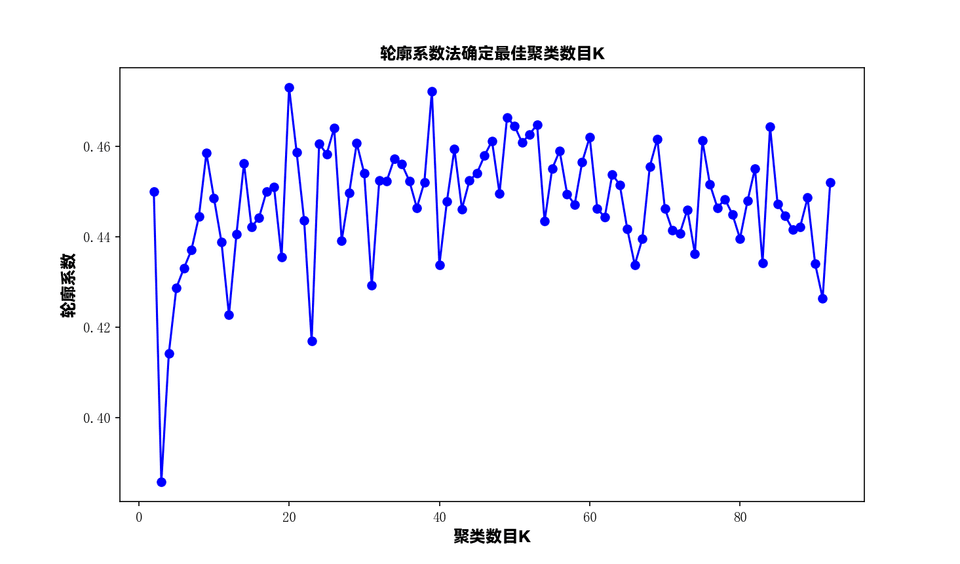
2.1.2 轮廓系数法

轮廓系数（Silhouette Coefficient）是一种衡量聚类效果好坏的统计指标，它结合了聚类的凝聚度（cohesion）和分离度（separation）。轮廓系数的取值范围是 [-1, 1]，值越大表示聚类效果越好。轮廓系数是通过以下两步计算得出的：

计算每个样本的轮廓系数：

凝聚度（a）：对于某个样本点，它是该样本到同一簇中所有其他样本的平均距离与该样本到最近簇中所有样本的平均距离的比值的倒数。凝聚度越大，表示样本与其簇内其他样本越紧密。
分离度（b）：对于某个样本点，它是该样本到最近簇中所有样本的平均距离。分离度越大，表示样本与其最近簇的差异越明显。对于每个样本 i，轮廓系数 $s (i)$ 计算如下： $s (i) = \frac {b (i) - a (i)}{\max (a (i), b (i))}$

计算整个数据集的平均轮廓系数：

对于所有样本的轮廓系数求平均，得到整个数据集的平均轮廓系数 $S$ ： $S = \frac {1}{n} \sum_{i=1}^{n} s (i)$ 其中 $n$ 是样本的总数。
如果 $s (i)$ 接近 1，表示样本点 i 与其同簇的点非常相似，而与不同簇的点差异很大，这是一个好的聚类。
如果 $s (i)$ 接近 - 1，表示样本点 i 很可能被分配到了错误的簇。
如果 $s (i)$ 接近 0，表示样本点 i 位于两个簇的边界上，对簇的分配没有明显的倾向。在确定 K-means 聚类中的最佳 K 值时，通常会对不同的 K 值计算轮廓系数，然后选择产生最高平均轮廓系数的 K 值。轮廓系数法是一种直观且广泛使用的方法，用于评估聚类的质量并选择最佳的聚类数目。

2.2 遗传算法求解

关于遗传算法中的一些关键概念：

名词解释

适应度函数 (Fitness Function)

适应度函数是评估遗传算法中每个个体适应度的函数。在旅行商问题（TSP）中，适应度通常与路径的总长度相关，目标是最小化路径的总长度。适应度函数的输出通常被用来选择个体进行繁殖，以产生下一代。

遗传算法 (Genetic Algorithm, GA)

遗传算法是一种启发式搜索算法，它模仿了自然选择的过程。它通过选择、交叉（或称为重组）、变异等操作在一定的迭代次数中进化出解决方案。

个体 (Individual)

在遗传算法中，个体代表问题的潜在解决方案。在 TSP 问题中，一个个体可以代表一条可能的旅行路径。

种群 (Population)

种群是一组个体，遗传算法在这些个体上进行操作。种群的多样性对于算法的搜索能力是非常重要的。

选择 (Selection)

选择是遗传算法中的一个步骤，它根据个体的适应度来选择它们进行繁殖。选择过程有助于将 “更好的” 个体传递到下一代。

交叉 (Crossover)

交叉是遗传算法中的一个关键步骤，它通过组合两个父代个体的部分来生成新的后代。这有助于在种群中引入新的遗传特征。

变异 (Mutation)

变异是遗传算法中的另一个重要步骤，它通过随机改变个体的某些基因来增加种群的遗传多样性。这有助于防止算法过早收敛到局部最优解。

交叉概率 (Crossover Probability, cxpb)

交叉概率是指导交叉操作发生的概率。较高的交叉概率意味着种群中更多的新个体将通过交叉生成。

变异概率 (Mutation Probability, mutpb)

变异概率是指导变异操作发生的概率。适度的变异概率有助于保持种群的多样性，防止算法陷入局部最优解。

迭代代数 (Number of Generations, ngen)

迭代代数是算法运行的代数，即算法重复选择、交叉和变异步骤的次数。算法可能会在达到这个迭代次数后停止，或者在找到满意的解之后停止。

锦标赛选择 (Tournament Selection)

锦标赛选择是一种选择方法，其中随机选择的一组个体（称为锦标赛）竞争，适应度最高的个体被选中进行繁殖。

适应度 (Fitness)

适应度是衡量个体解决问题能力的指标。在遗传算法中，个体的适应度通常用来决定它们是否被选中用于产生后代。

适应度景观 (Fitness Landscape)

适应度景观是一个抽象的概念，它描述了个体的适应度如何随着它们基因的变化而变化。在 TSP 问题中，适应度景观可能会非常复杂，因为个体的适应度（路径长度）会随着路径中城市顺序的微小变化而显著变化。

局部最优解 (Local Optima)

局部最优解是适应度在周围邻域中最高的个体。遗传算法的一个挑战是避免陷入局部最优解，而没有找到全局最优解。

全局最优解 (Global Optima)

全局最优解是所有可能解决方案中适应度最高的个体。遗传算法的目标是找到或接近全局最优解。

定义适应度函数

适应度函数用于评估个体（在 TSP 问题中，个体代表一条路径）的适应度，即个体解决问题的能力。在 TSP 问题中，我们希望找到一条最短的路径，因此适应度函数会计算路径的总长度，并将其作为适应度的相反数返回，因为我们希望最小化路径长度。

文档中的适应度函数定义如下：

def evalTSP(individual):
    distance = dist_matrix[individual[-1]][individual[0]]
    for gene1, gene2 in zip(individual[0:-1], individual[1:]):
        distance += dist_matrix[gene1][gene2]
    return distance,

这个函数首先计算最后一个城市回到起始城市的距离，然后遍历路径中的每个连续城市对，计算它们之间的距离，并将这些距离累加得到总路径长度。这个总长度就是个体的适应度，但因为我们希望最小化路径长度，所以返回的是其相反数。

实现遗传算法的操作

遗传算法包括选择（Selection）、交叉（Crossover）和变异（Mutation）三个主要操作：

选择（Selection）：选择适应度较高的个体用于下一代的繁殖。文档中使用锦标赛选择方法（tools.selTournament），其中指定了锦标赛大小为 3（tournsize=3）。
交叉（Crossover）：通过交换两个个体的部分基因来产生新的后代。文档中使用的是部分匹配交叉（tools.cxPartialyMatched）。
变异（Mutation）：随机改变个体的某些基因，以维持种群的多样性。文档中使用的是打乱索引变异（tools.mutShuffleIndexes），并设置了变异概率为 5%（indpb=0.05）。

设置种群大小、交叉概率、变异概率以及迭代代数

种群大小：种群大小（n=200）是指在遗传算法中同时考虑的个体数量。较大的种群可能包含更多的多样性，但计算成本也更高。
交叉概率（cxpb）：这是交叉操作在遗传算法中被应用的概率，文档中设置为 0.7，意味着 70% 的个体将通过交叉产生。
变异概率（mutpb）：这是变异操作在遗传算法中被应用的概率，文档中设置为 0.2，即 20% 的个体将经历变异。
迭代代数（ngen）：这是遗传算法运行的代数，文档中设置为 1000，意味着算法将迭代 1000 次，直到找到满意的解或达到预设的迭代次数。

这些参数的设置对算法的性能有很大影响，通常需要根据具体问题进行调整。在文档中，这些参数被用于 algorithms.eaSimple 函数，该函数实现了一个简单的遗传算法框架。

3. 实验设计

3.1 数据收集

使用高德地图、百度地图获取景点经纬度信息

3.2 数据预处理

对经纬度数据进行标准化处理。

景区名称	lang	lat
恭王府	116.3863	39.93721
八达岭长城风景名胜区	116.0168	40.35619
天坛公园	116.4109	39.88195
慕田峪长城	116.564	40.43086
故宫博物院	116.397	39.91806

3.3 聚类实现

使用 Python 的 sklearn 库进行聚类，并利用 matplotlib 库进行可视化。

3.3.1 轮廓系数法

# 轮廓系数zh.py
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
import matplotlib

# 设置中文字体
font_path = 'HarmonyOS_Sans_SC_Black.ttf'  # 中文字体文件路径
font = FontProperties(fname=font_path, size=12)
matplotlib.rc('font', family='SimSun')

# 从Excel文件中读取数据
data = pd.read_excel("5a.xlsx")

# 提取经度和纬度列数据
coordinates = data.iloc[:, 1:].values

# 设置聚类数目的范围
k_range = range(2, 93)  # 尝试聚类数目从2到93

# 存储每个K值对应的轮廓系数
silhouette_scores = []

# 计算每个K值对应的轮廓系数
for k in k_range:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(coordinates)
    labels = kmeans.labels_
    silhouette_scores.append(silhouette_score(coordinates, labels))

# 设置图形的大小和分辨率
fig, ax = plt.subplots(figsize=(10, 6), dpi=150)

# 绘制K值与轮廓系数的关系图
plt.plot(k_range, silhouette_scores, 'bo-')
plt.xlabel('聚类数目K', fontproperties=font)
plt.ylabel('轮廓系数', fontproperties=font)
plt.title('轮廓系数法确定最佳聚类数目K', fontproperties=font)
plt.show()

# 输出最大的轮廓系数及对应的K值
max_score = max(silhouette_scores)
best_k = k_range[silhouette_scores.index(max_score)]
print("最大的轮廓系数:", max_score)
print("对应的K值:", best_k)

3.3.2 聚类分析

# 聚类算法.py
import pandas as pd
import numpy as np
import openpyxl
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties, fontManager
from matplotlib.ticker import MultipleLocator

# 查找并选择正确的中文字体
font_path = None
for font in fontManager.ttflist:
    if 'SimSun' in font.name:
        font_path = font.fname
        break

# 设置中文字体
font = FontProperties(fname=font_path, size=12)

# 从Excel文件中读取数据
data = pd.read_excel("5a.xlsx")

# 提取经度和纬度列数据
coordinates = data.iloc[:, 1:].values

# 特征缩放
scaler = StandardScaler()
scaled_coordinates = scaler.fit_transform(coordinates)

# 设置聚类数目
k = 20

# 运行K-means算法
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(scaled_coordinates)

# 获取聚类标签
labels = kmeans.labels_
# 反向转换聚类中心坐标到原始范围
cluster_centers = scaler.inverse_transform(kmeans.cluster_centers_)

# 输出每个聚类中心坐标
for i, center in enumerate(cluster_centers):
    print("聚类中心", i+1, "经度:", center[0], "纬度:", center[1])

# 创建一个空的字典，用于存储每个聚类中心的点
cluster_points = {i: [] for i in range(k)}

# 假设名称在数据的第一列
names = data.iloc[:, 0].values

# 将每个数据点和其名称分配到相应的聚类中心
for i, label in enumerate(labels):
    cluster_points[label].append((names[i],) + tuple(coordinates[i]))

# 输出每个聚类中心的所有点到Excel文件
wb = openpyxl.Workbook()
for i in range(k):
    cluster_data = np.array(cluster_points[i])
    sheet = wb.create_sheet(title='Cluster {}'.format(i+1))
    for j, data in enumerate(cluster_data):
        sheet.cell(row=j+1, column=1).value = data[0]  # 名称
        sheet.cell(row=j+1, column=2).value = data[1]  # 经度
        sheet.cell(row=j+1, column=3).value = data[2]  # 纬度

# 保存Excel文件
wb.save('cluster_points.xlsx')

# 创建一个新的Excel文件来存储聚类中心的位置
wb_centers = openpyxl.Workbook()
sheet = wb_centers.active
sheet.title = 'Cluster Centers'
for i, center in enumerate(cluster_centers):
    sheet.cell(row=i+1, column=1).value = "聚类中心" + str(i+1)"Cluster " + str(i+1) +"_order"
    sheet.cell(row=i+1, column=2).value = center[0]  # 经度
    sheet.cell(row=i+1, column=3).value = center[1]  # 纬度

# 保存新的Excel文件
wb_centers.save('cluster_centers.xlsx')

# 设置图形的大小和分辨率
fig, ax = plt.subplots(figsize=(12, 9), dpi=300)

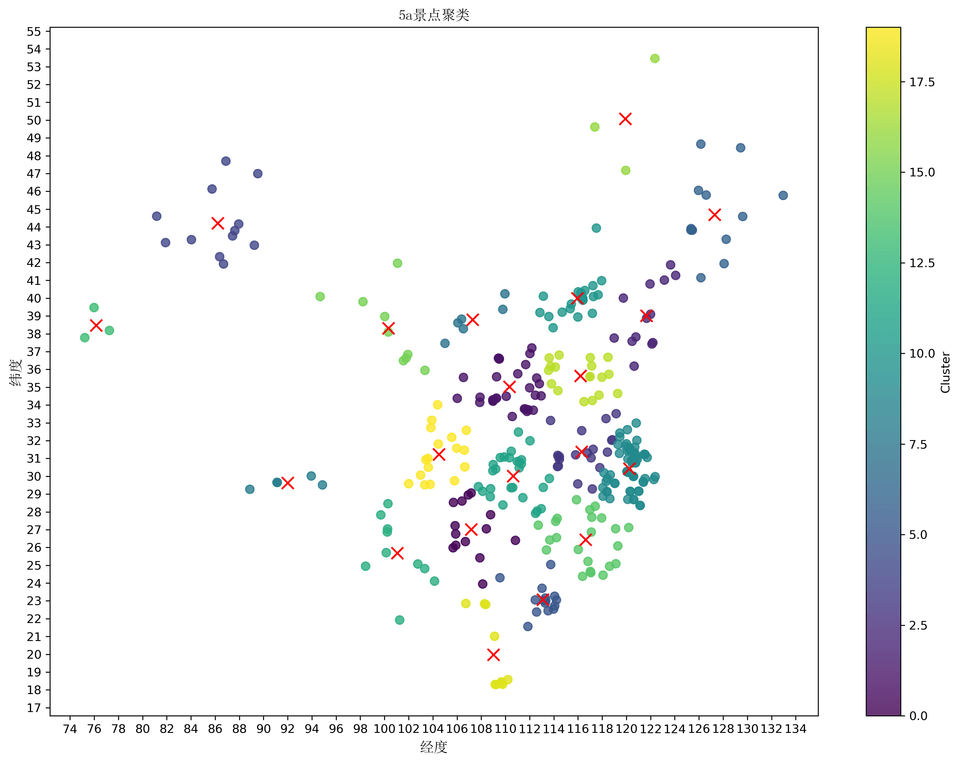
# 绘制数据点散点图
scatter = ax.scatter(
    coordinates[:, 0],
    coordinates[:, 1],
    c=labels,
    cmap='viridis',
    alpha=0.8,
    s=50,
    linewidths=1
)

# 绘制聚类中心点散点图
ax.scatter(
    cluster_centers[:, 0],
    cluster_centers[:, 1],
    marker='x',
    c='red',
    s=100
)

# 自定义图表
ax.set_xlabel('经度', fontproperties=font)
ax.set_ylabel('纬度', fontproperties=font)
ax.set_title('5a景点聚类', fontproperties=font)

# 设置刻度线密度
ax.xaxis.set_major_locator(MultipleLocator(2))
ax.yaxis.set_major_locator(MultipleLocator(1))

# 添加颜色条图例
cbar = plt.colorbar(scatter)
cbar.set_label('Cluster')

# 调整图表布局并显示图表
plt.tight_layout()
plt.show()

3.4 遗传算法实现

使用 deap 库实现遗传算法。

import pandas as pd
import numpy as np
from scipy.spatial import distance_matrix
from deap import creator, base, tools, algorithms
import os
# 读取数据
df = pd.read_excel('cluster_centers.xlsx', header=None)

# 计算距离矩阵
dist_matrix = distance_matrix(df.iloc[:, 1:].values, df.iloc[:, 1:].values)

# 定义适应度函数
def evalTSP(individual):
    distance = dist_matrix[individual[-1]][individual[0]]
    for gene1, gene2 in zip(individual[0:-1], individual[1:]):
        distance += dist_matrix[gene1][gene2]
    return distance,

# 创建遗传算法相关的类和函数
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creator.create("Individual", list, fitness=creator.FitnessMin)

toolbox = base.Toolbox()
toolbox.register("indices", np.random.permutation, len(df))
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.indices)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)

toolbox.register("mate", tools.cxPartialyMatched)
toolbox.register("mutate", tools.mutShuffleIndexes, indpb=0.05)
toolbox.register("select", tools.selTournament, tournsize=3)
toolbox.register("evaluate", evalTSP)

# 运行遗传算法
pop = toolbox.population(n=200)
hof = tools.HallOfFame(1)
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("Avg", np.mean)
stats.register("Std", np.std)
stats.register("Min", np.min)
stats.register("Max", np.max)

pop, log = algorithms.eaSimple(pop, toolbox, cxpb=0.7, mutpb=0.2, ngen=1000, stats=stats, halloffame=hof, verbose=True)

# 输出最佳路径
best_path_names = [df.iloc[i, 0] for i in hof[0]]
print('最佳路径为：', best_path_names)
# 创建一个新的数据框来存储最佳路径
best_path_df = pd.DataFrame(best_path_names, columns=['地点'])
# 确保/order目录存在
if not os.path.exists('order'):
    os.makedirs('order')
# 将最佳路径写入到Excel文件中
best_path_df.to_excel('order/cluster_centers.xlsx', index=False)

3.5 数据处理代码

3.5.1 循环运行遗传算法

import pandas as pd
import numpy as np
from scipy.spatial import distance_matrix
from deap import creator, base, tools, algorithms
import os

# 定义一个函数，接受一个Excel文件名作为参数，执行遗传算法，并将结果保存到一个新的Excel文件中。
def run_ga_on_excel_file(filename):
    print(f"开始处理文件：{filename}")
    # 读取数据
    df = pd.read_excel(filename, header=None)

    # 计算距离矩阵
    dist_matrix = distance_matrix(df.iloc[:, 1:].values, df.iloc[:, 1:].values)

    # 定义适应度函数
    def evalTSP(individual):
        distance = dist_matrix[individual[-1]][individual[0]]
        for gene1, gene2 in zip(individual[0:-1], individual[1:]):
            distance += dist_matrix[gene1][gene2]
        return distance,

    # 创建遗传算法相关的类和函数
    creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
    creator.create("Individual", list, fitness=creator.FitnessMin)

    toolbox = base.Toolbox()
    toolbox.register("indices", np.random.permutation, len(df))
    toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.indices)
    toolbox.register("population", tools.initRepeat, list, toolbox.individual)

    toolbox.register("mate", tools.cxPartialyMatched)
    toolbox.register("mutate", tools.mutShuffleIndexes, indpb=0.05)
    toolbox.register("select", tools.selTournament, tournsize=3)
    toolbox.register("evaluate", evalTSP)

    # 运行遗传算法
    pop = toolbox.population(n=200)
    hof = tools.HallOfFame(1)
    stats = tools.Statistics(lambda ind: ind.fitness.values)
    stats.register("Avg", np.mean)
    stats.register("Std", np.std)
    stats.register("Min", np.min)
    stats.register("Max", np.max)

    pop, log = algorithms.eaSimple(pop, toolbox, cxpb=0.7, mutpb=0.2, ngen=1000, stats=stats, halloffame=hof, verbose=True)

    # 输出最佳路径
    best_path_names = [df.iloc[i, 0] for i in hof[0]]
    print('最佳路径为：', best_path_names)
    # 创建一个新的数据框来存储最佳路径
    best_path_df = pd.DataFrame(best_path_names, columns=['地点'])
    # 确保/order目录存在
    if not os.path.exists('order'):
        os.makedirs('order')
    # 将最佳路径写入到Excel文件中
    output_filename = 'order/' + os.path.splitext(os.path.basename(filename))[0] + '_order.xlsx'
    best_path_df.to_excel(output_filename, index=False)
    print(f"处理完成，结果已保存到：{output_filename}")

# 获取文件夹中的所有文件名
folder_name = 'excel'  # 替换为你的文件夹名
filenames = os.listdir(folder_name)

# 对于每个Excel文件，运行遗传算法
for filename in filenames:
    if filename.endswith('.xlsx'):
        run_ga_on_excel_file(os.path.join(folder_name, filename))

3.5.2 拆分 excel

import os
import openpyxl

# 打开包含所有工作表的Excel文件
wb = openpyxl.load_workbook('cluster_points.xlsx')

# 确保/excel目录存在
if not os.path.exists('excel'):
    os.makedirs('excel')

# 遍历工作簿中的每个工作表
for sheet in wb.sheetnames:
    # 创建一个新的工作簿
    new_wb = openpyxl.Workbook()
    # 将当前工作表的数据复制到新的工作簿中
    new_ws = new_wb.active
    for row in wb[sheet].iter_rows(values_only=True):
        new_ws.append(row)
    # 将新的工作簿保存为一个新的Excel文件，文件名为原工作表的名称
    new_wb.save(f'excel/{sheet}.xlsx')

3.5.3 excel 转 csv

import os
import pandas as pd

# 获取当前目录下的所有文件
files = os.listdir()

# 检查csv文件夹是否存在，如果不存在，创建它
if not os.path.exists('../csv'):
    os.makedirs('../csv')

for file in files:
    # 检查文件是否为Excel文件
    if file.endswith('.xlsx') or file.endswith('.xls'):
        # 读取Excel文件
        df = pd.read_excel(file)
        # 将DataFrame转换为CSV文件，指定编码为utf-8
        df.to_csv('../csv/' + file.replace('.xlsx', '.csv').replace('.xls', '.csv'), index=False, encoding='utf-8')

3.5.4 合并 csv

import pandas as pd

# 创建一个空的DataFrame
df_combined = pd.DataFrame()

# 读取包含文件名的CSV文件，跳过第一行
with open('cluster_centers.csv', 'r') as f:
    next(f)  # 跳过第一行
    for line in f:
        filename = line.strip() + '.csv'  # 获取文件名

        # 读取CSV文件
        df = pd.read_csv(filename)

        # 将内容添加到df_combined中
        df_combined = pd.concat([df_combined, df])

# 查看合并后的DataFrame
print(df_combined)
# 保存合并后的DataFrame为CSV文件，使用GBK编码
df_combined.to_csv('combined.csv', index='false',encoding='GBK')#index='false'，不显示排序

4. 结果

最大的轮廓系数为 0.47303329125259336，对应的 K 值为 20。
聚类中心的坐标被计算并输出。

聚类中心 1 经度: 107.15918657142856 纬度: 27.01445992857143
聚类中心 2 经度: 110.31887722580645 纬度: 35.03142016129032
聚类中心 3 经度: 121.64953453846154 纬度: 39.016035076923075
聚类中心 4 经度: 116.29445795238095 纬度: 31.369955714285712
聚类中心 5 经度: 86.21727425 纬度: 44.20822241666667
聚类中心 6 经度: 113.08218666666667 纬度: 23.07359466666667
聚类中心 7 经度: 127.2935646923077 纬度: 44.69739769230769
聚类中心 8 经度: 107.28551116666667 纬度: 38.7997335
聚类中心 9 经度: 91.9894854 纬度: 29.6192552
聚类中心 10 经度: 120.24057079365079 纬度: 30.424040920634923
聚类中心 11 经度: 115.95039617391305 纬度: 39.988152782608694
聚类中心 12 经度: 110.63040137037036 纬度: 30.00380159259259
聚类中心 13 经度: 101.0548785 纬度: 25.6775198
聚类中心 14 经度: 76.158255 纬度: 38.47950566666667
聚类中心 15 经度: 116.63771369565217 纬度: 26.43329856521739
聚类中心 16 经度: 100.32991055555556 纬度: 38.31310277777778
聚类中心 17 经度: 119.89828533333333 纬度: 50.08402233333333
聚类中心 18 经度: 116.1950486111111 纬度: 35.630323777777775
聚类中心 19 经度: 109.0134903 纬度: 19.984577899999998
聚类中心 20 经度: 104.51067864705882 纬度: 31.229174529411765

遗传算法得到的最短路径被保存至 Excel 文件。

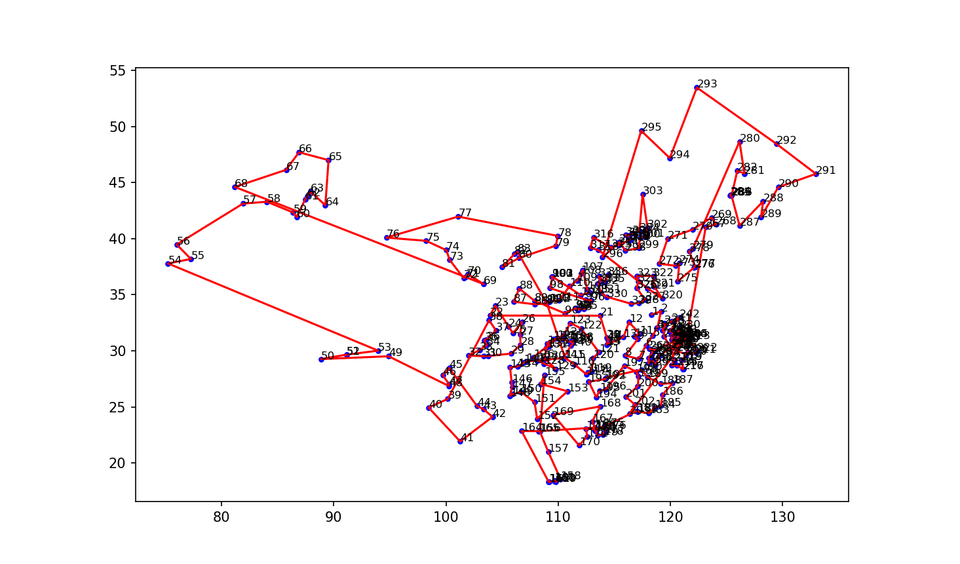
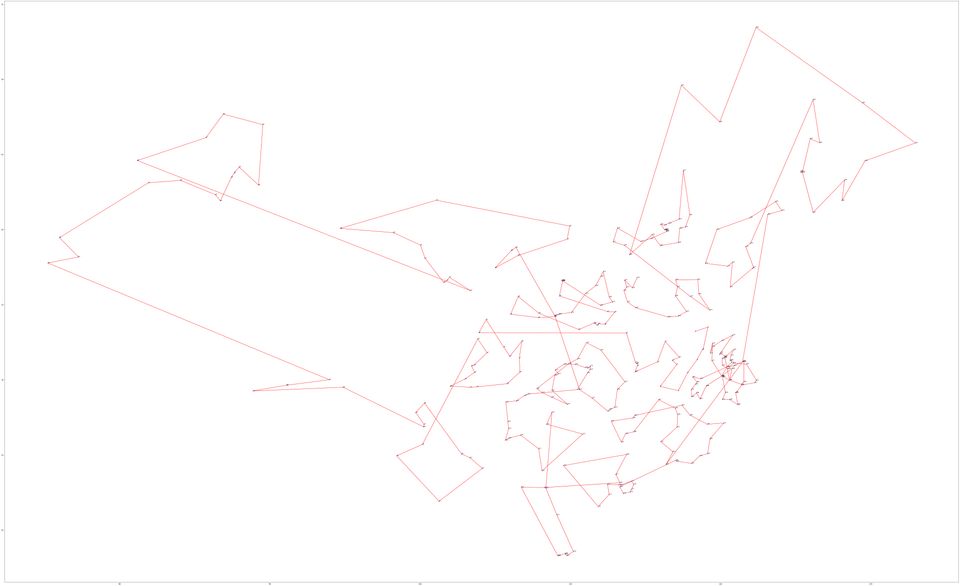
宿迁泗洪县洪泽湖湿地公园
淮安市周恩来故里旅游景区
南京钟山风景名胜区—中山陵园风景区
南京夫子庙秦淮风光带
方特旅游区
九华山景区
江西省景德镇市古窑民俗博览区
江西省九江市庐山风景名胜区
天柱山景区
万佛湖景区
肥西三河古镇
八里河旅游区
天堂寨景区
武汉东湖景区
武汉市黄鹤楼公园
黄陂木兰文化生态旅游区（木兰草原）
黄陂木兰文化生态旅游区（木兰云雾山）
黄陂木兰文化生态旅游区（木兰山）
湖北省武汉市黄陂木兰文化生态旅游区
黄陂木兰文化生态旅游区（木兰天池）
嵖岈山风景区
九寨沟风景名胜区
陇南官鹅沟旅游景区
剑门蜀道剑门关旅游景区
阆中古城
巴中市光雾山景区
朱德故里景区
邓小平故里旅游区
重庆大足石刻景区
乐山大佛景区
峨眉山风景名胜区
泸定海螺沟冰川森林公园
碧峰峡旅游景区
安仁古镇景区
汶川特别旅游区
青城山--都江堰旅游景区
北川羌城旅游区
黄龙国家级风景名胜区
大理崇圣寺三塔文化旅游区
腾冲火山热海旅游区
中国科学院西双版纳热带植物园景区
普者黑旅游景区
昆明市石林风景名胜区
昆明世博园旅游区
甘孜州稻城亚丁景区
迪庆香格里拉普达措景区
丽江玉龙雪山景区
丽江古城景区
雅鲁藏布大峡谷景区
扎什伦布寺景区
布达拉宫
大昭寺
巴松措风景旅游区
帕米尔旅游区
泽普县金湖杨景区
喀什古城景区
喀拉峻景区
伊犁哈萨克自治州那拉提旅游风景区
巴音布鲁克景区
博斯腾湖景区（大河口）
乌鲁木齐天山大峡谷
博斯腾湖景区（莲海世界）
天山天池风景区
葡萄沟景区
可可托海景区
喀纳斯景区
世界魔鬼城景区
赛里木湖风景名胜区
永靖县炳灵寺世界文化遗产旅游
互助土族故土园旅游区
青海湖景区
塔尔寺旅游区
海北州阿咪东索景区
张掖七彩丹霞景区
嘉峪关文物景区
敦煌鸣沙山?月牙泉景区
胡杨林景区
响沙湾旅游景区
成吉思汗陵陵游区
水洞沟旅游区
沙坡头景区
镇北堡西部影城
沙湖旅游区
西安城墙·碑林历史文化景区
西安曲江大雁塔·大唐芙蓉园景区
太白山旅游景区
麦积山景区
国家重点风景名胜区崆峒山
法门文化景区
金丝峡景区
鸡冠洞景区
老君山风景区
老界岭—恐龙遗迹园景区
洛阳白云山景区
尧山景区
少林景区
龙门石窟
黄帝陵景区
延安革命纪念地景区（中共中央西北局旧址）
延安革命纪念地景区（枣园革命旧址）
延安革命纪念地景区（杨家岭革命旧址）
延安革命纪念地景区（延安革命纪念馆）
延安革命纪念地景区（宝塔山景区）
龙潭大峡谷
云台山5A拓展景区—青天河、神农山景区
皇城相府
平遥古城景区
绵山景区
洪洞大槐树寻根祭祖园
乡宁县云丘山景区
华山景区
秦始皇帝陵博物院
陕西华清宫文化旅游景区
大明宫国家遗址公园
张家界武陵源—天门山旅游区(天门山旅游区)
常德市桃花源旅游区
湘潭市韶山旅游区
长沙市花明楼景区
长沙市岳麓山-橘子洲旅游区
岳阳楼-君山岛旅游区
咸宁市赤壁古战场景区
襄阳市古隆中景区
武当山风景区
神农架生态旅游区
重庆巫山小三峡—小小三峡
重庆武隆喀斯特旅游区（天生三桥·仙女山·芙蓉洞）
重庆彭水阿依河景区
重庆酉阳桃花源景区
湘西州矮寨·十八洞·德夯大峡谷景区
重庆黔江濯水景区
恩施州利川腾龙洞景区
恩施大峡谷景区
重庆云阳龙缸景区
重庆奉节白帝城——瞿塘峡景区
恩施州神农溪纤夫文化旅游区
屈原故里文化旅游区
三峡人家景区
宜昌市三峡大瀑布旅游区
三峡大坝
宜昌市长阳清江画廊景区
张家界武陵源—天门山旅游区（武陵源旅游区）
重庆南川金佛山景区
重庆万盛黑山谷景区
重庆江津四面山景区
遵义市赤水丹霞旅游区
毕节市百里杜鹃景区
毕节市织金洞景区
安顺市黄果树旅游景区
安顺市龙宫旅游景区
贵阳市花溪青岩古镇景区
黔南州荔波樟江旅游景区
都安民族博物馆
新宁崀山旅游区
黔东南州镇远古城旅游景区
铜仁市江口梵净山生态旅游景区
南宁青秀山风景旅游区
北海涠洲岛南湾鳄鱼山景区
海南分界洲岛旅游区
蜈支洲岛旅游区
槟榔谷黎苗文化旅游区
海南呀诺达雨林文化旅游区
南山文化旅游区
大小洞天旅游区
德天跨国瀑布景区
（梧州动物园）
广州市白云山风景区
清远市连州地下河旅游景区
韶关市丹霞山景区
山岔湾景区
阳江市海陵岛大角湾海上丝路旅游区
江门市开平碉楼文化旅游区
肇庆市星湖旅游景区
佛山市西樵山景区
广州市长隆旅游度假区
惠州市罗浮山景区
惠州市西湖旅游景区
深圳市观澜湖休闲度假区
深圳市华侨城旅游度假区
中山市孙中山故里旅游区
佛山市长鹿旅游休博园
福建土楼（永定）旅游景区
福建土楼（南靖）旅游景区
厦门市鼓浪屿旅游区
泉州市清源山景区
莆田市湄洲岛妈祖文化旅游区
福州市三坊七巷历史文化街区景区
宁德市福鼎太姥山风景区
宁德市屏南县白水洋·鸳鸯溪旅游区
武夷山市风景名胜区
江西省上饶市龟峰景区
江西省宜春市明月山旅游区
江西省萍乡市武功山景区
南岳衡山旅游区
郴州市东江湖旅游区
株洲市炎帝陵景区
江西省吉安市井冈山风景旅游区
江西省南昌市滕王阁旅游区
江西省鹰潭市龙虎山景区
江西省抚州市资溪大觉山景区
三明市泰宁风景旅游区
江西省瑞金市“共和国”摇篮旅游区
龙岩市古田旅游区
梅州市雁南飞茶田景区
东方明珠广播电视塔
上海科技馆
天一阁·月湖景区
溪口—滕头景区
鲁迅故里.沈园景区(鲁迅故里）
杭州西湖风景名胜区
杭州西湖景区
横店影视城5A级景区
浙江省金华市东阳市横店影视城
仙都景区
神仙居景区
神仙居景区
温州市雁荡山风景旅游管委会
浙江省温州市乐清市雁荡山景区
浙江省台州市天台山景区
天台山风景名胜区
溪口滕头旅游景区
浙江省舟山市普陀区普陀山风景旅游区
舟山市普陀山风景名胜区管理委会
上海野生动物园
苏州市周庄古镇景区
浙江省嘉兴市桐乡市乌镇景区
乌镇景区
苏州市吴中太湖旅游区
无锡灵山景区
中央电视台无锡影视基地三国水浒景区
南通市濠河景区
苏州市沙家浜·虞山尚湖旅游区
苏州园林景区
苏州市金鸡湖景区
苏州市同里古镇景区
湖州市南浔古镇景区
西溪湿地公园景区
常州市天目湖景区
扬州瘦西湖风景区
镇江市句容茅山风景区
镇江市金山·焦山·北固山景区
泰州姜堰溱湖旅游景区
盐城市大丰中华麋鹿园景区
常州市中国春秋淹城旅游区
常州市环球恐龙城休闲旅游区
无锡市惠山古镇景区
无锡市太湖鼋头渚景区
绍兴鲁迅故里·沈园景区
鲁迅故里.沈园景区（沈园景区）
南湖旅游区
嘉兴市南湖旅游区
杭州西溪国家湿地公园
杭州西溪国家湿地公园?洪园
淳安县千岛湖风景区
杭州市千岛湖景区
江郎山-廿八都旅游区
根宫佛国文化旅游区
衢州开化根宫佛国文化旅游区
江西省上饶市三清山风景名胜区
江西省上饶市江湾景区
皖南古村落
古徽州文化旅游区
黄山景区
绩溪龙川景区
南浔古镇景区
西塘古镇景区
中国共产党一大·二大·四大纪念馆
辽宁千山景区
本溪水洞景区
沈阳市植物园（沈阳世博园）
盘锦红海滩国家风景廊道景区
山海关景区
黄河口生态旅游区
烟台市龙口南山景区
烟台市蓬莱阁（三仙山·八仙过海）旅游区
崂山风景区
威海华夏城景区
威海市刘公岛景区
大连老虎滩海洋公园
辽宁省大连市金石滩景区
五大连池风景区
太阳岛风景区
肇东市昌盛生态农业观光园景区
长影世纪城旅游区
长春伪满皇宫博物院
长春世界雕塑园
长春净月潭景区
高句丽文物古迹旅游景区
六鼎山文化旅游区
长白山景区
牡丹江镜泊湖风景名胜区
虎头旅游景区
汤旺河林海奇石景区
漠河市北极村景区
阿尔山一柴河旅游景区
满洲里市中俄边境旅游区
西柏坡景区
野三坡景区
白洋淀景区
天津古文化街旅游区（津门故里）
天津盘山风景名胜区
清东陵
承德避暑山庄及周围寺庙景区
阿斯哈图石林景区
承德市滦平县金山岭长城景区
慕田峪长城
十三陵
八达岭长城风景名胜区
颐和园
圆明园遗址公园
北京市奥林匹克公园
故宫博物院
恭王府
天坛公园
清西陵景区
白石山景区
云冈石窟
忻州市代县雁门关风景区
忻州市五台山风景名胜区
沂蒙山旅游区
连云港市花果山风景区
临沂市萤火虫水洞·地下大峡谷旅游区
青州古城旅游区
天下第一泉
泰山景区
济宁市曲阜明故城（三孔）旅游区
微山湖旅游区
台儿庄古城景区
徐州市云龙湖景区
永城市芒砀山旅游景区
清明上河园
新乡八里沟景区
太行山八泉峡景区
林州市红旗渠·太行大峡谷景区
涉县娲皇宫
安阳殷墟景区
永年区广府古城旅游区

5. 可视化

绘制了聚类中心和数据点的散点图，展示了聚类效果。

输出总顺序和绘图

import pandas as pd
import geopandas as gpd
import matplotlib.pyplot as plt
from shapely.geometry import Point

# 读取Excel文件
df = pd.read_excel('顺序.xlsx')

# 创建GeoDataFrame
gdf = gpd.GeoDataFrame(df, geometry=gpd.points_from_xy(df.lang, df.lat))

# 绘制地点的经纬度
fig, ax = plt.subplots(figsize=(100, 100),dpi=150)
gdf.plot(ax=ax, color='blue',markersize=10)

# 绘制旅行路径
ax.plot(gdf['lang'], gdf['lat'], color='red')

# 为每个地点添加数字标签
for i, point in gdf.iterrows():
    ax.text(point['lang'], point['lat'], str(i+1),fontsize=8)
    
plt.show()